
In that form, the longitudinal shear is a force per unit length along the section, and Q is the shear force in the section. I learnt it as longitudinal shear = Q A y / I.
How is Q defined for case (b)?Īs preamble, I note that the equation for this shear stress / force / flow is something that seems to suffer from almost everyone adopting a different nomenclature. In short, my definition of Q has broken down spectacularly. Thus, a horizontal plane cannot be defined co-planer to the 2 vertical shear planes to denote that I want to calculate the shear flow along this horizontal plane. The two shear planes are vertical planes that run along the longitudinal axis of the beam. Now let's apply this understanding of Q to figure b in the first picture. In that diagram, the shear plane is a plane running along the longitudinal axis of the beam at a height $y$ above the neutral axis. This Q value was explained to me to be the area of the cross section of the beam on the opposite side of the desired horizontal shear plane.
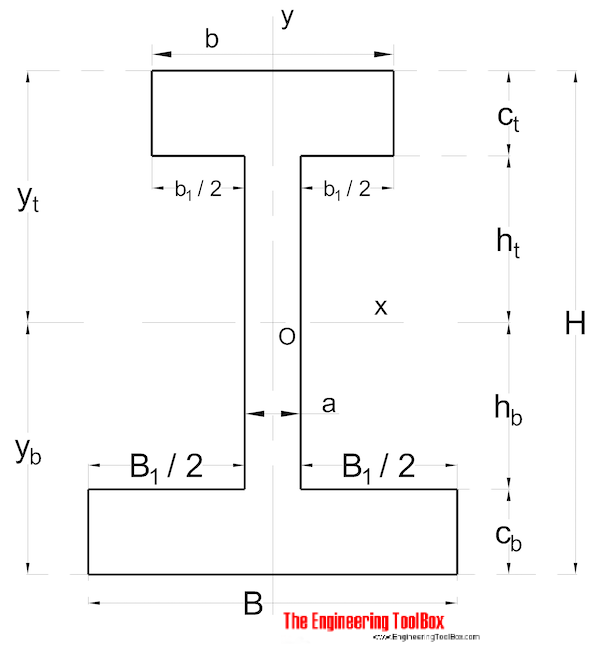
To calculate this shear stress, a first moment of area (Q) needed to be calculated. I have no good justification for this choice.Įdit: More information: Before I was introduced to the concept of shear flow, I was taught how to make shear stress calculations at any given height above or below the centroid of a beam cross section. Based on other sources I have consulted, the area I should choose is the area of the board in the center of the two upright members. The two shear planes are perpendicular to the plane that separates A' from the rest of the member, meaning the definition I used for the first case on the left simply doesn't apply. I am confused about how to choose Q on the right hand side scenario. A is the area of the top board since the cross sectional area of that board corresponds to the area on the opposite side of the shear plane to the centroid of the member. The simple analogy is that of a rod.Consider the two scenarios in this picture: This is because the axis of rotation is closer to the center of mass of the system in (b). We see that the moment of inertia is greater in (a) than (b). Using the parallel-axis theorem eases the computation of the moment of inertia of compound objects. Refer to (Figure) for the moments of inertia for the individual objects. In both cases, the moment of inertia of the rod is about an axis at one end. In (b), the center of mass of the sphere is located a distance R from the axis of rotation.

In (a), the center of mass of the sphere is located at a distanceįrom the axis of rotation. Since we have a compound object in both cases, we can use the parallel-axis theorem to find the moment of inertia about each axis. The radius of the sphere is 20.0 cm and has mass 1.0 kg.

The rod has length 0.5 m and mass 2.0 kg. Find the moment of inertia of the rod and solid sphere combination about the two axes as shown below.


 0 kommentar(er)
0 kommentar(er)
